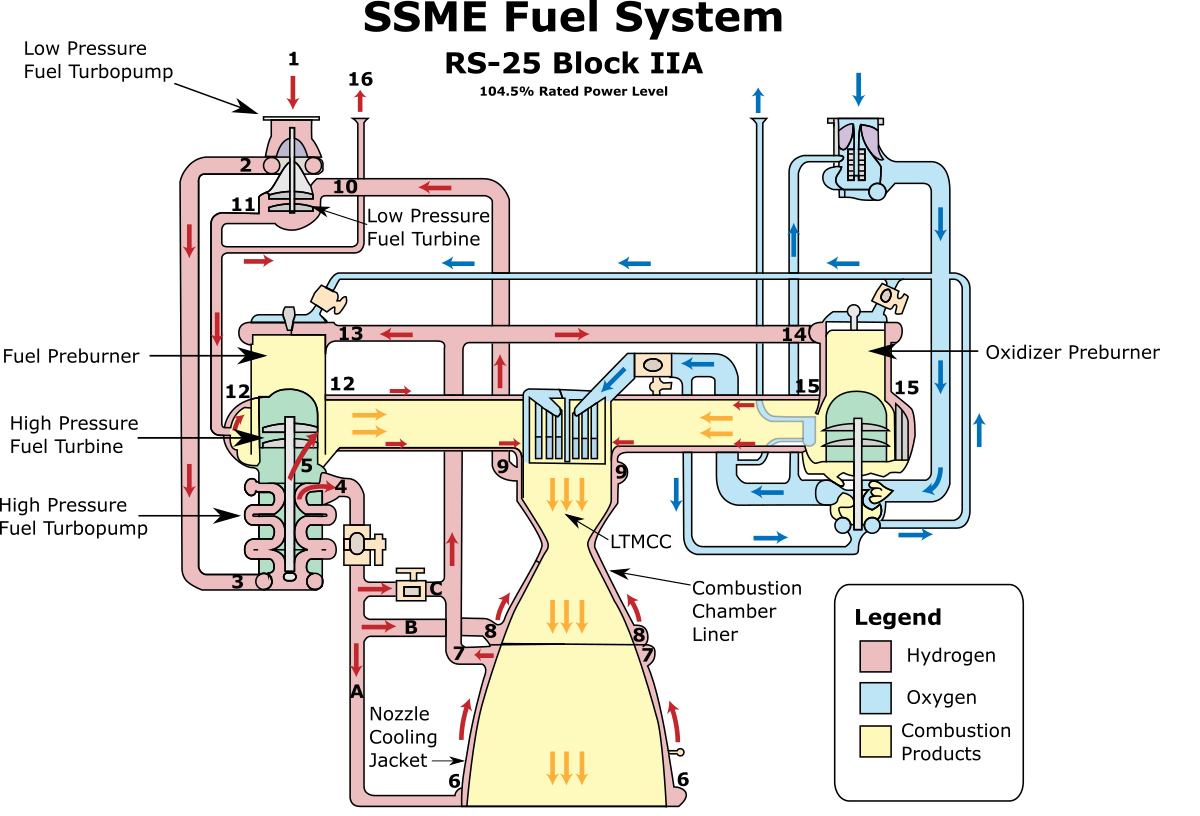
Figure 4.1.1: SSME Fuel System Schematic [1]
The equations of state developed in Section 2 and the combustion model developed in Section 3 provide all the necessary tools to perform a high-level analysis of the SSME’s turbomachinery. We begin with the Low Pressure Fuel Turbopump.
Low Pressure Fuel Turbopump
Liquid hydrogen enters this pump at Station 1 from the external tank with a known pressure, known temperature, and known mass flow rate (set by the overall mixture ratio, see Equation 3.1.1). We assume the desired output pressure from the pump is known, along with the pump’s efficiency, $\eta$. The task is to determine how much power, $\dot W$, is required to drive the pump under these conditions. Since input pressure and temperature are known, the Helmholtz equation of state can be used to calculate the input density and input enthalpy, $h_1$, with Equation 2.2.3. Input entropy, $s_1$, can be calculated with Equation 2.2.4.
There are not many known quantities on the output side of the pump at Station 2. Liquid hydrogen is compressible under certain conditions (see Figure 2.2.1), so it is not always valid to assume that $\rho_1 = \rho_2$. This pump is only 71.3 percent efficient, so not all of the input shaft work is converted into pressure. Some of the shaft work is converted into heat that raises output temperature of the fluid. Therefore it is not safe to assume $T_1 = T_2$. Known input and output conditions are shown below on Figure 4.1.2
Figure 4.1.2
Now the First Law of Thermodynamics can be applied to simplify the above system in a similar manner to that described in Section 3.2. First, we assume that there is no significant increase in fluid kinetic energy or gravitational potential energy between either side of the pump. This means that $V_1=V_2$ and $Z_1 = Z_2$. We assume there is no heat transfer through walls of the pump, but there is shaft work, $\dot W$, being applied to pressurize the fluid. Conservation of mass requires that $\rho_1V_1A_1 = \rho_2V_2A_2$. With these assumptions the First Law of Thermodynamics reduces to:
Enthalpy is a state function, so we need a method to solve for one additional state variable ($\rho_2$ or $T_2$) in order to find $h_2$ using the Helmholtz correlation for hydrogen, Equation 2.1.7. To do this we turn to a definition for pump efficiency, $\eta_P$:[4]
It is important to note that in the above equation there are two different output enthalpies, $h_{2s}$ and $h_{2a}$, that must be accounted for. These enthalpies correspond to two different states: the isentropic state $2s$ (a theoretical construct that assumes no entropy generation as fluid travels through the pump), and the actual state $2a$ reached after accounting for effects of entropy. These states are shown on the following h-s diagram:
Figure 4.1.3: Low Pressure Fuel Turbopump h-s Diagram
Figure 4.1.3 shows that $s_{2s} = s_1$. $P_1$ and $P_2$ are also known. Although these two known state variables theoretically should allow us to calculate the remaining thermodynamic properties at Stations 1 and 2, these variables don’t line up with Helmholtz equation of state developed in Section 2.2. The Helmholtz model requires two of the following three variables to be known: temperature, pressure, or density. In this case we only know pressure and entropy. There are three steps to resolve this problem.
Step 1:
Establish a multi-variable Newton-Raphson scheme similar to the one described in Section 3.3 and solve for $T_{2s}$, $\rho_{2s}$, and $h_{2s}$ iteratively using the known values of $P_1$, $P_2$, $s_1$, and $s_{2s}$ as inputs.
First, guess initial values for $T_{2s,i}$ and $\rho_{2s,i}$ and use these values as the center points in a central finite difference scheme to solve for $\frac{\partial{s_{2s}}}{\partial{T}}$ and $\frac{\partial{s_{2s}}}{\partial{\rho}}$. The corresponding centered finite differences are shown below.
The function $s_2\left(T, \rho\right)$ is modeled by Equation 2.2.4.
Next, establish finite differences for $\frac{\partial{P_{2s}}}{\partial{T}}$ and $\frac{\partial{P_{2s}}}{\partial{\rho}}$ in a similar manner. The corresponding centered finite differences are shown below.
The function $P_2\left(T, \rho\right)$ is modeled by Equation 2.2.2.
The resulting matrix equation becomes:
where x and y are intermediate values. This system can be solved for $x$ and $y$ using a Gauss elimination routine.[47] Once $x$ and $y$ are known, updated values for $T_{2s,i+1}$ and $\rho_{2s,i+1}$ can be determined as follows:
The updated temperature and density values are plugged into the Helmholtz model to calculate refined pressure, entropy, and enthalpy values and use these to establish relative error:
The average error is calculated as $\left(\text{error}_1 +\text{error}_2 \right)/2$.
Step 2: Solve for $h_{2a}$ and $\dot W$
We can now plug the isentropic enthalpy value into Equation 4.1.2 and solve for the actual output enthalpy value accounting for effects of entropy:
$$h_{2a}=\left(h_{2s,i+1}-h_1\right)/\eta_P+h_1$$
The amount of power required to drive the turbopump is the determined via Equation 4.1.11:
Step 3: Solve for $T_{2a}$
We now have four known state variables on the output side of the pump: $h_{2a}$, $\rho_{2s}$, $s_{2a}$, and $P_2$. Unfortunately, selecting any combination of two of these variables still does not give enough information to yield an explicit solution for $T_{2a}$. Once again we must rely on an iterative method. The procedure is very similar to that described in Step 2.
First, guess initial values for $T_{2a,i}$ and $\rho_{2a,i}$ and use these values as the center points in a central finite difference scheme to solve for $\frac{\partial{h_{2a}}}{\partial{T}}$ and $\frac{\partial{h_{2a}}}{\partial{\rho}}$. The corresponding centered finite differences are shown below.
The function $h_2\left(T, \rho\right)$ is modeled by Equation 2.2.3.
Next, use the finite differences established for $\frac{\partial{P_{2}}}{\partial{T}}$ and $\frac{\partial{P_{2}}}{\partial{\rho}}$ (Equations 4.1.5 and 4.1.6) to construct the following system:
where $x$ and $y$ are intermediate values. This system can be solved for $x$ and y$$ using a Gauss elimination routine. Once x and y are known, updated values for $T_{2a,i+1}$ and $\rho_{2a,i+1}$ can be determined as follows:
We then plug the updated temperature and density values into the Helmholtz model to calculate refined pressure and enthalpy values, then use these to establish relative error:
The average error is calculated as $\left(\text{error}_1 +\text{error}_2 \right)/2$.
Results of this calculation are tabulated below. This model predicts the Low Pressure Fuel Turbopump’s output power requirement to within 3% of actual values. While these values are not perfect, they are sufficient for preliminary design estimates and validate both the procedure developed in this section and the Helmholtz equation of state developed in Section 2.2 .
| Calculated | Actual Value [2] | Relative Error (%) | |
|---|---|---|---|
| $T_2$ $[K]$ | 22.31 | 23.7 | 5.86 |
| $\dot W$ $[Hp]$ | 3421 | 3330 | 2.73 |
Table 4.1.1: Low Pressure Fuel Turbopump Calculation Results
Low Pressure Fuel Turbine
Now we know how much power is required to operate the Low Pressure Fuel Turbopump. The question then becomes how to generate that power. The Low Pressure Fuel Turbine accomplishes this task. Liquid hydrogen enters the turbine at Station 10, as shown above on Figure 4.1.1 The turbine rotors extract energy from the flow (in the form of pressure and temperature drop between Stations 10 and 11) and convert it to shaft work which is then used to spin the compressor in the Low Pressure Fuel Turbopump. We assume the flow inlet conditions at Station 10 are known. We also know the maximum allowable pressure drop between Stations 10 and 11 (established by the minimum required inlet pressure into the main combustion chamber). These conditions are shown below on Figure 4.1.4.
Figure 4.1.4
A key difference between the turbine analysis and pump analysis is that in the case of the turbine we do not know the mass flow rate through the system. We need to solve for the mass flow rate required to generate the 3330 HP demanded by the Low Pressure Fuel Pump. The solution procedure is almost identical to that of used for the Low Pressure Fuel Pump. All of the equations used in Steps 1 and 3 are still valid. In Step 2 a definition for turbine efficiency, $\eta_T$, is introduced:[4]
where again 11a and 11s correspond to the respective actual and isentropic states. These states are plotted below on an h-s diagram:
Figure 4.1.5
The required mass flow rate through the turbine then becomes:
The negative sign on $\dot W$ accounts for the fact that work is being extracted from the system. Results of this calculation are tabulated below. This model predicts the Low Pressure Fuel Turbine’s output temperature and required mass flow requirement to within 10% of actual values. While far from perfect, this is sufficient for “back of the envelope” preliminary design estimates.
| Calculated | Actual Value [2] | Relative Error (%) | |
|---|---|---|---|
| $T_{11}$ $[K]$ | 249.2 | 255.4 | 2.43 |
| $\dot m_{11}$ $[\frac{kg}{s}]$ | 14.47 | 13.2 | 9.62 |
Table 4.1.2: Low Pressure Fuel Turbine Calculation Results